About

In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal

Filters play an important role in sound design, we will see in this section how to apply filters with parameters that we can modulate, we will especially recreate generic filters such as low-pass, high-pass etc.

How-to

Low-pass filter

A low-pass filter is a filter that passes signals with a frequency lower than a certain cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency.

We will use the low-pass filter as a prototype filter, which mean that we will build all the other filters from this one.

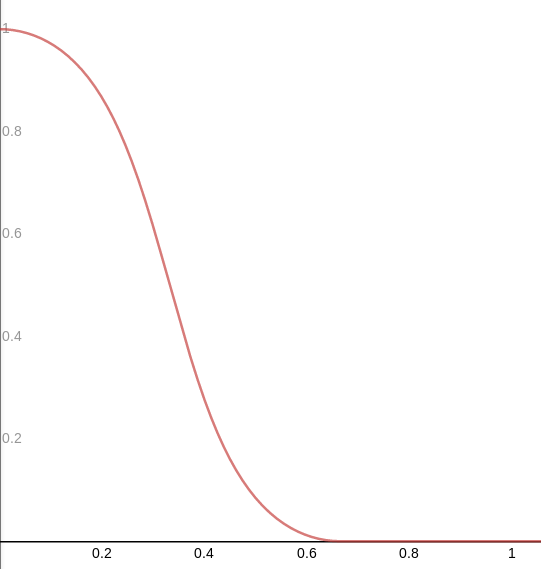
Graph of the lpf(x, 0., 1.5); function

float adsr(float t, vec4 v, float s) {
  v.xyw = max(vec3(2.2e-05), v.xyw);
  float ta = t/v.x;
  float td = max(s, 1.0-(t-v.x)*(1.0-s)/v.y);
  float tr = (1.0 - max(0.0,t-(v.x+v.y+v.z))/v.w);
  return max(0.0, min(ta, tr*td));
}

// low-pass filter
// x is the current normalized position
// c is the cutoff position
// s is the slope
float lpf(float x, float c, float s) {
  return .5 + .5 *(atan(s*cos(3.141592653 * min(max((x-c) * s,0.),1.)))/atan(s));
}

void main () {
  // we will need the current normalized coordinates
  vec2 uv = gl_FragCoord.xy / resolution.xy;

  float l = 0.;
  float r = 0.;

  const float harmonics = 16.;

  for (int k = 0; k < 16; k += 2) {
    vec4 data = keyboard[k];

    float kfrq = data.x;
    float kvel = data.y;
    float ktim = data.z;
    float kchn = data.w;

    if (kfrq == 0.) {
      break; 
    }

    // the htoy function take a frequency as argument
    // and return its position on the canvas
    // we then normalize the position
    // the base frequency of our note will be directly used as the cutoff frequency
    float cutoff = htoy(kfrq) / resolution.y;
    for (float i = 1.; i < harmonics; i += 1.) {
      // our slope factor, high frequencies will be attenuated
      float slope = 3.;
      float f = lpf(uv.y, cutoff, slope);

      float attack = 0.05;
      float decay = 0.6;
      float sustain = 0.;
      float release = 0.25;
      float dec_amp = 0.;
      float env = kvel * adsr(ktim, vec4(attack, decay, sustain, release), dec_amp);

      l += fline(kfrq * i) * f * env;
      r += fline(kfrq * i) * f * env;
    }
  }

  fragColor = vec4(l, r, 0., 1.);
  synthOutput = vec4(l, r, 0., 0.);
}

Now that a low-pass filter has been made, we can build all the other filters easily

High-pass filter

// the high pass filter is just an inversed LPF
float hpf(float x, float c, float s) {
  return lpf(1. - x, 1. - c, s); 
}

Band-pass filter

// a bpf is obtained by combining a lpf and hpf
float bpf(float x, float c, float s) {
  return lpf(x, c, s) * hpf(x, c, s);
}

Band-reject filter

// band-reject
float brf(float x, float c, float s) {
  return (1. - lpf(x, c, s)) + (1. - hpf(x, c, s));
}

Example with all filters

float adsr(float t, vec4 v, float s) {
  v.xyw = max(vec3(2.2e-05), v.xyw);
  float ta = t/v.x;
  float td = max(s, 1.0-(t-v.x)*(1.0-s)/v.y);
  float tr = (1.0 - max(0.0,t-(v.x+v.y+v.z))/v.w);
  return max(0.0, min(ta, tr*td));
}

float lpf(float x, float c, float s) {
  return .5 + .5 *(atan(s*cos(3.141592653 * min(max((x-c) * s,0.),1.)))/atan(s));
}

// the high pass filter is just an inversed LPF
float hpf(float x, float c, float s) {
  return lpf(1. - x, 1. - c, s); 
}

// a bpf is obtained by combining a lpf and hpf
float bpf(float x, float c, float s) {
  return lpf(x, c, s) * hpf(x, c, s);
}

// band-reject
float brf(float x, float c, float s) {
  return (1. - lpf(x, c, s)) + (1. - hpf(x, c, s));
}

void main () {
  vec2 uv = gl_FragCoord.xy / resolution.xy;

  float l = 0.;
  float r = 0.;

  const float harmonics = 16.;

  for (int k = 0; k < 16; k += 2) {
    vec4 data = keyboard[k];

    float kfrq = data.x;
    float kvel = data.y;
    float ktim = data.z;
    float kchn = data.w;

    if (kfrq == 0.) {
      break; 
    }

    float cutoff = htoy(kfrq) / resolution.y;

    float slope = 3. + sin(ktim * 4.);

    // compute the filters
    // we modulate the cutoff parameter
    // to show how the filters behave
    float fhp = hpf(uv.y, cutoff + sin(ktim * 1.25) / 2., slope);
    float fbp = bpf(uv.y, cutoff + sin((ktim - 1.) * 1.25) / 2., slope * 1.25);
    float fbr = brf(uv.y, cutoff + sin((ktim - 2.) * 1.25) / 2., slope * 1.5);

    float attack = 0.5;
    float decay = 0.5;
    float sustain = 0.;
    float release = 0.25;
    float dec_amp = 0.;

    // we offset the keyboard time
    // of the total amount of time the envelope will take
    // so that our sounds start when the previous end
    float env1 = kvel * adsr(ktim, vec4(attack, decay, sustain, release), dec_amp);
    float env2 = kvel * adsr(ktim - 1., vec4(attack, decay, sustain, release), dec_amp);
    float env3 = kvel * adsr(ktim - 2., vec4(attack, decay, sustain, release), dec_amp);

    for (float i = 1.; i < harmonics; i += 1.) {
      float f = kfrq * i;

      // we build three sounds offseted by the envelope
      // with each filters assigned
      l += fline(f) * fhp * env1;
      r += fline(f) * fhp * env1;

      l += fline(f) * fbp * env2;
      r += fline(f) * fbp * env2;

      l += fline(f) * fbr * env3;
      r += fline(f) * fbr * env3;
    }
  }

  fragColor = vec4(l, r, 0., 1.);
  synthOutput = vec4(l, r, 0., 0.);
}

Those functions are not perfect, they don't have a resonance parameter and the filters cutoff/slope need to be adjusted for HPF/BPF/BRF because the attenuation is not per octaves.